Click for Larger Image
Why the Normal Distribution has a "Bell-Curve" Shape
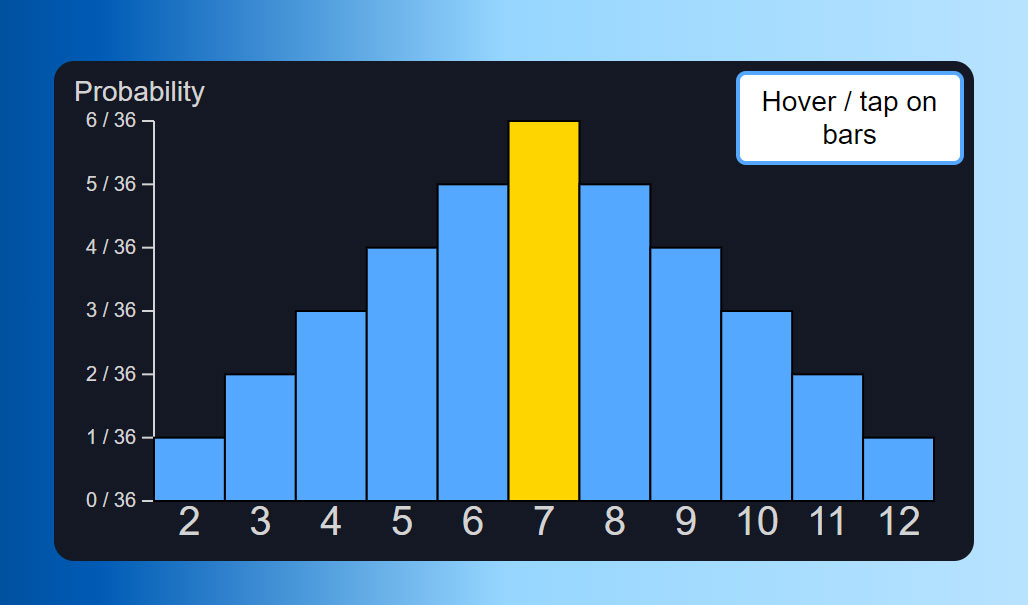
The normal distribution certainly has a beautiful shape. And in our dataful world, it's everywhere. Heights, weights, neurons firing, the apparent brightness of stars... they all mysteriously fall into line on the "bell curve".
Read article